| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- v8 tracing
- LLVM
- 안티디버깅
- 난독화
- android inject
- anti debugging
- pinpoint
- linux debugging
- Linux packer
- tracerpid
- Obfuscator
- Injection
- pthread
- on stack replacement
- OSR
- TLS
- custom packer
- initial-exec
- on-stack replacement
- Linux custom packer
- linux thread
- so inject
- LLVM 난독화
- thread local storage
- Android
- apm
- uftrace
- v8 optimizing
- LLVM Obfuscator
- tracing
- Today
- Total
Why should I know this?
SuperOptimization Study 본문
* 이 글은 작성 중 입니다. 왜 작성 중인 글을 올려놓냐면 그래야 동기 부여가 되서 귀차니즘을 극복할 수 있기 때문입니다. *
* 양해 바라고 양질의 글로 보답하겠습니다. *
0. Super Optimization 개요
peephole optimization 에 대한 정의는 wiki에서 확인 가능
https://en.wikipedia.org/wiki/Peephole_optimization
Peephole optimization - Wikipedia
From Wikipedia, the free encyclopedia Compiler optimization technique Peephole optimization is an optimization technique performed on a small set of compiler-generated instructions; the small set is known as the peephole or window.[1] Peephole optimization
en.wikipedia.org
1. Super Optimization ?

왜 이런 개념이 등장했는가? peephole 최적화의 정의에서 확인 가능하다시피 여기서 파생될 수 있는 최적화는 경우의 수가 너무 많음. 그럼 이런 경우의 수를 모조리 Compiler 최적화 단에서 한땀한땀 추가하는 것에 대한 필요성에 대한 회의감이 들 수 밖에 없고, 때문에 Peephole 최적화는 상당한 근거가 뒷받침되서 개선 당위성이 입증되야함.
100개의 최적화를 추가해서 거둘 수 있는 성능이 1이라면 이것도 의미가 있을 수 있지만 컴파일 시의 비용문제로 배제되게 된다는 뜻임.
이걸 개선할 방법이 없을까? 하는 고민이 자연스럽게 나오게 되고 그 결과 Super Optimization 이라는 기법에 대한 고안이 등장.
2. Super Optimization
Super Optimization (이하 "suop")의 개념은 간단함
https://llvm.org/devmtg/2011-11/Sands_Super-optimizingLLVMIR.pdf

LLVM 을 기반으로 생성되는 IR 들을 분석해서 이를 simplification - 최적화 - 할 수 있는지 여부를 검증해서 LLVM에 추가하겠다는 것.
검증 표현 유형과 관련해서는 문서 41장에서 다음과 같이 다루고 있다.
- Constant Folding
- zext x < 0 -> 0
- Reduce to sub-expression
- ((x + z) * nsw y) / y -> x + z
- Unused variables
- x - (x + y) -> 0 - y
- Rule reduction
- 본문 생략
유관 Pass는 LLVM의 InstSimplify, InstCombine 로 소스코드 내부에 주석으로 다양하게 표현되어 있으므로 참고하면 된다.
https://llvm.org/doxygen/InstructionCombining_8cpp_source.html
LLVM: lib/Transforms/InstCombine/InstructionCombining.cpp Source File
static bool combineInstructionsOverFunction(Function &F, InstructionWorklist &Worklist, AliasAnalysis *AA, AssumptionCache &AC, TargetLibraryInfo &TLI, TargetTransformInfo &TTI, DominatorTree &DT, OptimizationRemarkEmitter &ORE, BlockFrequencyInfo *BFI, Pr
llvm.org
예를 들면 이렇게 주석이 달려있다.
// if C1 and C2 are constants.
3. SOUPER
앞서 살펴봤듯 Super Optimization은 Havest라고 불리는 최적화 가능할 것 같은 일련의 Instruction chunk를 찾아내고 그를 검증하는 것이 중요하다. SOLVER 라고 불리는 툴과 이를 활용한 SOUPER 가 등장하기 전까지 이런 과정은 미리 최적화 할 수 있는 경우를 작성해야 하는데 위 문서에는 Rule Reduction이라고 나온 내용이 여기 해당.
하지만 SOLVER 가 활용가능한 수준까지 고도화 되면서 SOUPER 에서는 이를 활용해 RULE 없이 최적화 할 수 있는 방식을 도입했다.
이게 어떻게 가능한가?
다음과 같은 코드가 있다고 했을때, (물론 LLVM에서 최적화가 되는 코드)
int main()
{
char a, b, c, d, e;
c = a ^ b;
d = b ^ c;
e = c ^ d;
return e;
}여기서, d 는 (b ^ (a ^ b)) 이고 llvm 에 따르면 xor은 Commutive 이므로 ( https://llvm.org/doxygen/IR_2Instruction_8h_source.html#l00590 ) Commutative operators satisfy: (x op y) === (y op x) 라고 한다. 그러므로 위 식은 (b ^ a ^ b ) - << 이거 이모티콘 아님! - 에서 (a ^ b ^ b) 로 바꿀 수 있다. 그러면 같은 값을 xor 하므로 무조건 0이 떨어지고 a ^ 0 은 곧 a.
그러면 c 는 (a ^ b) 이므로 e = (a ^ b ^ a) 가 된다. << 이것도 이모티콘 아님;
다시 a ^ a ^ b 로 바꾸면 0 ^ b 이므로 e = b 가 된다.
결과적으로 이 함수가 최적화 되면 다 날리고 b를 리턴하는 코드만 남기게 된다.
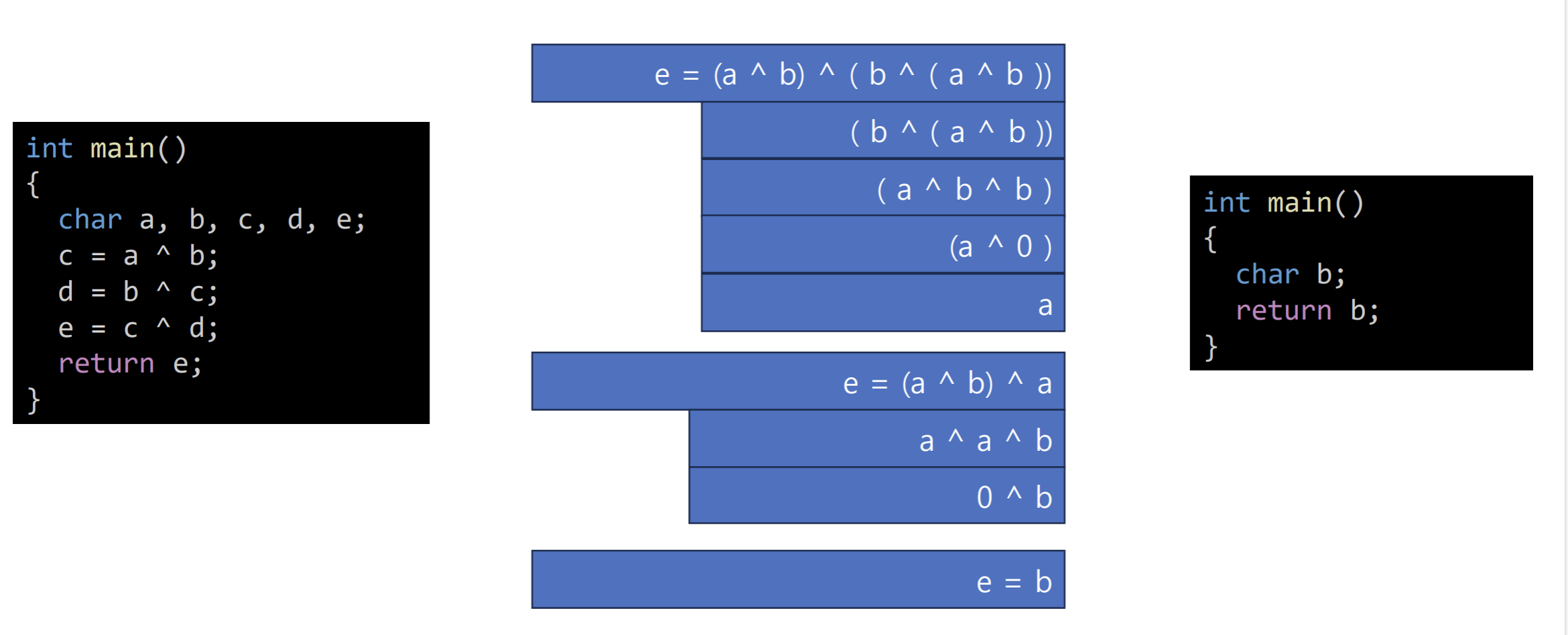
근데 중요한건 이게 아니고,
이처럼 LLVM의 peephole 최적화 단계에서는
위와 유사한 과정을 거쳐 최종적으로 LLVM 최적화에 반영된 최적화 케이스만이 컴파일 할 때 최적화 되게 되는데,
SOUPER 에서는 미반영된 peephole 최적화를 자동으로 발굴해서 적용하고자 Solver를 활용하였고
이것이 중요한 것이다.
그러면 Solver 를 통해 어떻게 자동화 할 수 있느냐?
Solver라는 툴은 주어진 수식에서 자동으로 "해" = 답 을 찾아주는 기능을 가진 도구입니다.
1. SOUPER에서는 먼저 IR 을 SOUPER IR 로 변경한다.
%0:i32 = var
%1:i32 = var
%2:i32 = xor %0, %1
%3:i32 = xor %1, %2
%4:i32 = xor %2, %3
2. Cadidates 를 만든다. -> 난해해서 설명이 틀릴 수 있음.
Candidates 는 AST 와 유사한 Instruction Set 이다.
candidates : [ 0]
%0:i32 = var ; 0
=================================
candidates : [ 1]
%0:i32 = var ; 1
=================================
candidates : [ 2]
%0:i32 = var ; 0
%1:i32 = var ; 1
%2:i32 = xor %0, %1
=================================
candidates : [ 3]
%0:i32 = var ; 1
%1:i32 = var ; 0
%2:i32 = xor %1, %0
%3:i32 = xor %0, %2
=================================
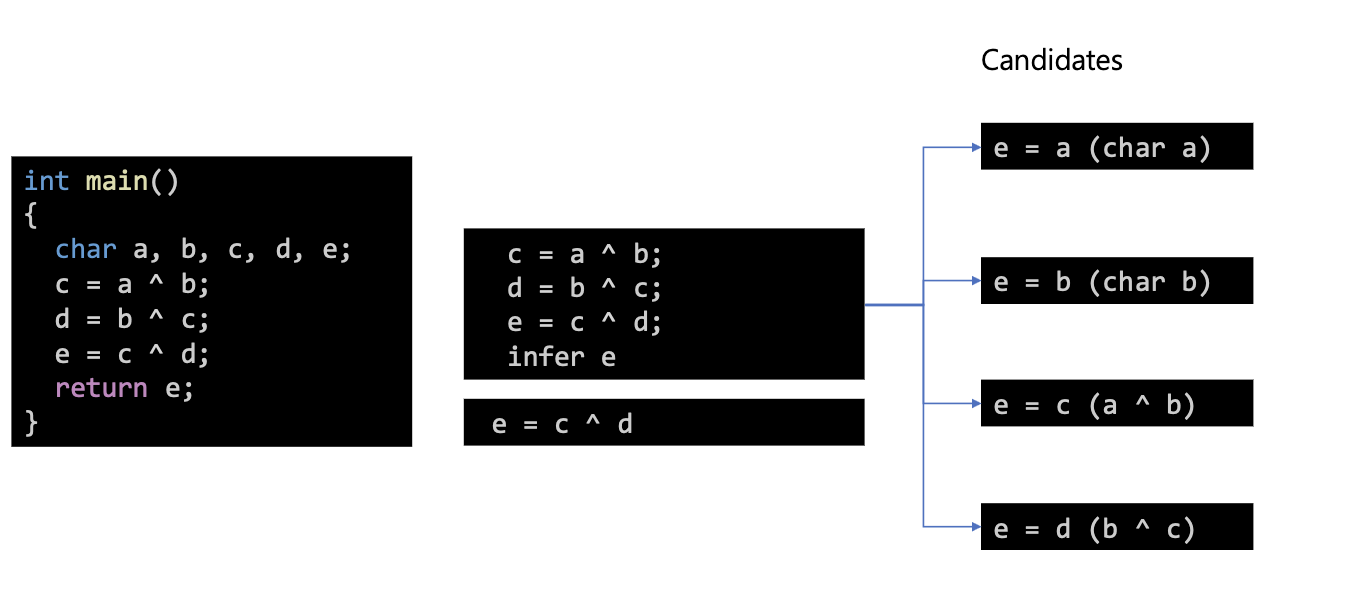
3. 각 Cadidates 를 SMT syntax로 바꾼다.
[ConcreteCandidateSat] QUERY : (set-logic QF_BV )
(declare-fun a0 () (_ BitVec 32) )
(declare-fun a1 () (_ BitVec 32) )
(assert (let ( (?B1 a1 ) (?B2 a0 ) ) (let ( (?B3 (bvxor ?B2 ?B1 ) ) ) (let ( (?B4 (bvxor ?B1 ?B3 ) ) ) (let ( (?B5 (bvxor ?B3 ?B4 ) ) ) (let ( (?B6 (= ?B1 ?B5 ) ) ) (= false ?B6 ) ) ) ) ) ) )
(check-sat)
(exit)

CHAT-GPT의 해석

4. SMT syntax 를 기반으로 Solver에 질의한다.
(여기서는 KLEE를 기반으로 활용하기 위해 KLEE 표현식으로 바꿔서 KLEE에 던진다. )
; KLEE expression:
; (Eq N0:(Read w32 0 a1) (Xor w32 N1:(Xor w32 (Read w32 0 a0) N0) (Xor w32 N0 N1)))
5. Query 결과를 반영한다. -> 설명이 틀릴 수 있음.
위의 SMT 쿼리를 해석하면 다음과 같다 (chatgpt 도움)
| 주어진 코드에서 검사하려는 제약은 다음 부분에 나와 있습니다: (assert (let ((?B1 a1) (?B2 a0)) (let ((?B3 (bvxor ?B2 ?B1))) (let ((?B4 (bvxor ?B1 ?B3))) (let ((?B5 (bvxor ?B3 ?B4))) (let ((?B6 (= ?B1 ?B5))) (= false ?B6)))))))
|
과정을 정리하면 다음과 같다.
위 C 코드는 다음같은 수식이고 (a ^ b) ^ ( b ^ ( a ^ b )) 이 수식에서 사용하는 변수는 a, b 둘이다.
결과적으로 위에서 설명한 과정의 마지막 과저에 이르면,
B6 = ( b != ( (a ^ b) ^ ( b ^ ( a ^ b )) )) 이 된다.
결과는, query is UNSAT, guess works 이라고 나오며,
b가 ( (a ^ b) ^ ( b ^ ( a ^ b )) ) 이 아닐 수 없다는 뜻, 그러므로 이 경우 ( (a ^ b) ^ ( b ^ ( a ^ b )) ) 가 b 인가? 하는
추정이 맞게 된다.
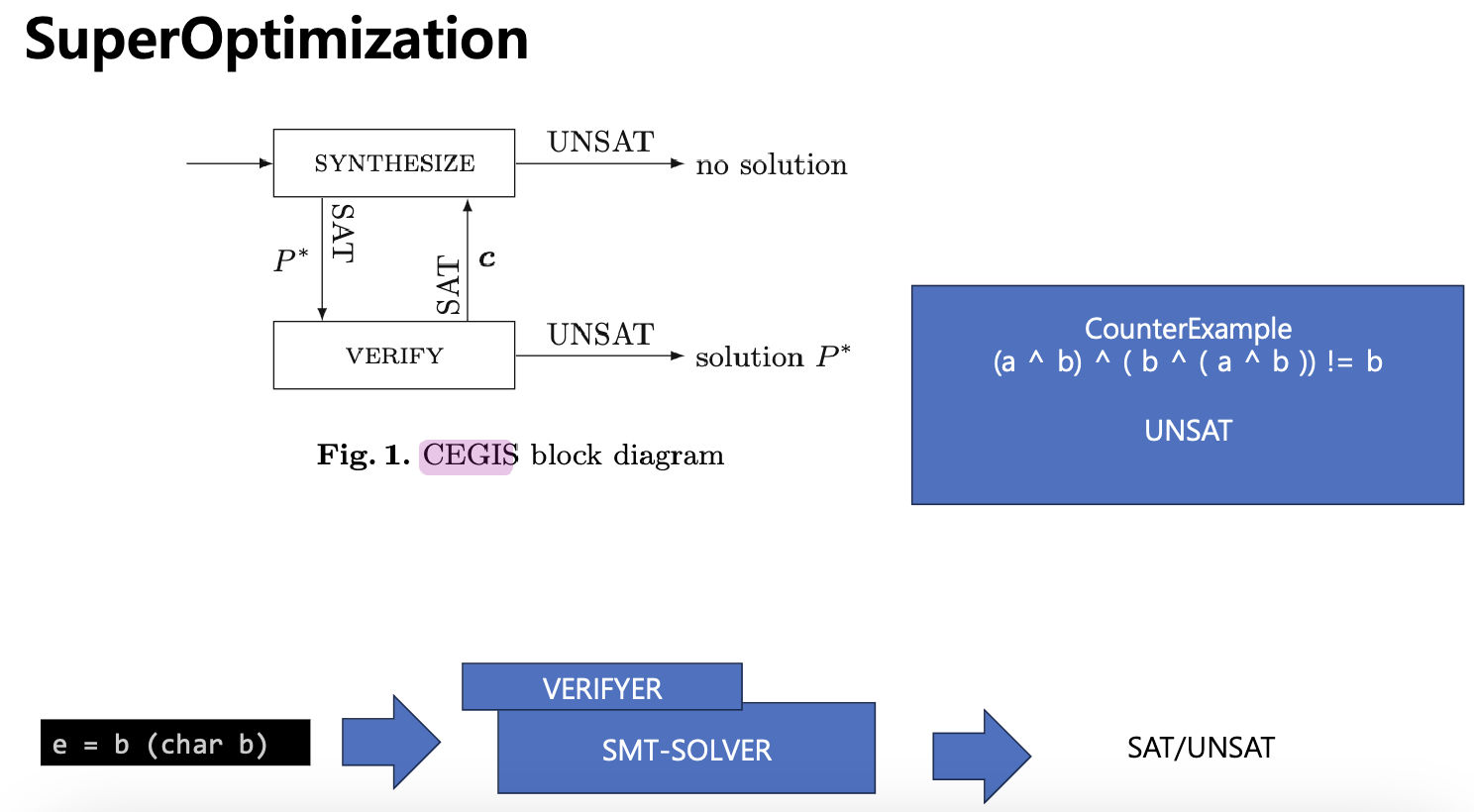
이처럼 가정에 대한 반증을 찾는 방식으로 가정을 증명하는 방식을 "반증 기반 유도 합성 = CEGIS (counterexample guided inductive synthesis ) " 이라고 한다.
SMT Solver에게 (a ^ b) ^ ( b ^ ( a ^ b )) ) ! = b 라는 질의를 던지는데, 이것이 바로 반증이 성립하는 경우를 Solver에게 찾아달라고 요청하는 것이다. 만약 반증이 성립하는 경우가 있으면 Solver는 SAT 를 반환하게 되며, (a ^ b) ^ ( b ^ ( a ^ b )) ) 라는 식이 b가 아닌 경우가 존재한다는 뜻이 된다. UNSAT은 반대로, b가 아닌 경우를 찾을 수 없다. 라는 의미가 된다.
4. SOUPER & Concolic Execution.
3에서 KLEE에 대한 언급이 잠깐 나왔는데 KLEE 를 잠깐 언급하자면 KLEE는 Symbolic Execuiton 기반의 소프트웨어 검증 툴이다. 마찬가지로 이 툴도 Solver와 연계하여 경로 탐색 및 오류 검출 기능을 제공한다.
중요한 것은 Symbolic -> Concolic 에 대한 개념이다.
https://en.wikipedia.org/wiki/Concolic_testing
Concolic testing - Wikipedia
From Wikipedia, the free encyclopedia Software verification technique Concolic testing (a portmanteau of concrete and symbolic, also known as dynamic symbolic execution) is a hybrid software verification technique that performs symbolic execution, a classi
en.wikipedia.org
https://swtv.kaist.ac.kr/publications/c815bcf4acfcd559d68cc9c0-concolicd14cc2a4d305.pdf
이 기법은 본래는 Software verication 연구 쪽에서 활용하는 기법인데, SOUPER 의 기법이 이와 유사한 맥락이 있다.
관련 내용은 다른 글에서 다루도록 하겠습니다.
5. 한계점
AlphaDev 논문에서는 머신런닝을 통한 알고리즘 최적화 연구 및 성과에 대한 발표가 있었다. 이 논문에서는 머신런닝을 통한 최적화 연구 전에 관련 연구 동향에 대해서 간단하게 몇 가지 언급하고 있는데, 이들이 말하는 한계점에 대해 알아보고자 한다.
논문에는 3가지 방향에 대해 평을 달아놨는데, Souper나 SMT 관련해서는 둘만 보면 된다.
First, enumerative search techniques include brute-force program enumeration as well as implicit enumeration using symbolic theorem proving. These approaches search through the space of programs to find a solution based on a predefined set of programs, heuristic and/ or cost function. These approaches struggle to span large regions of program space, especially as the size and complexity of the program increases.
Third, symbolic search approaches can also be implemented to optimize assembly programs. These include SAT solvers, SMT solvers and Mixed Integer Programs (MIPs). However, these approaches suffer from scaling issues. For example, classical solvers require a problem to be translated into a certain canonical form. It usually requires an expert in the said solvers and a substantial amount of time to find an efficient formulation. In addition, for any new modification of the problem, this has to be repeated. Classical solvers are also hard to parallelize and thus, it is challenging to leverage more hardware to speed up the solving process. Another symbolic search algorithm is Cholorphyll that implements a multi-phase approach. It first requires as input a source program with partition annotations that specify where code and data reside. Then, a layout synthesizer maps program fragments onto physical cores to minimize computational costs. The code is then separated into per-core program fragments and the program fragments are compiled into machine code. At this point, a superoptimizer optimizes each of these fragments.
-. 프로그램의 규모와 복잡성이 증가함에 따라 프로그램 공간의 넓은 영역을 포괄하는 데 어려움을 겪습니다.
-. 고전적인 솔버는 문제를 특정 표준 형식으로 변환해야 합니다. 일반적으로 해당 솔버에 대한 전문가가 필요하며 효율적인 공식을 찾는 데 상당한 시간이 소요됩니다.
역시 가장 큰 문제는 SMT Solver를 사용하기 위한 편의성이 많이 좋아졌다고 해도 부족하다는 점이다.
6. 결론 - 머신런닝 원툴이면 세상 다 끝나나?
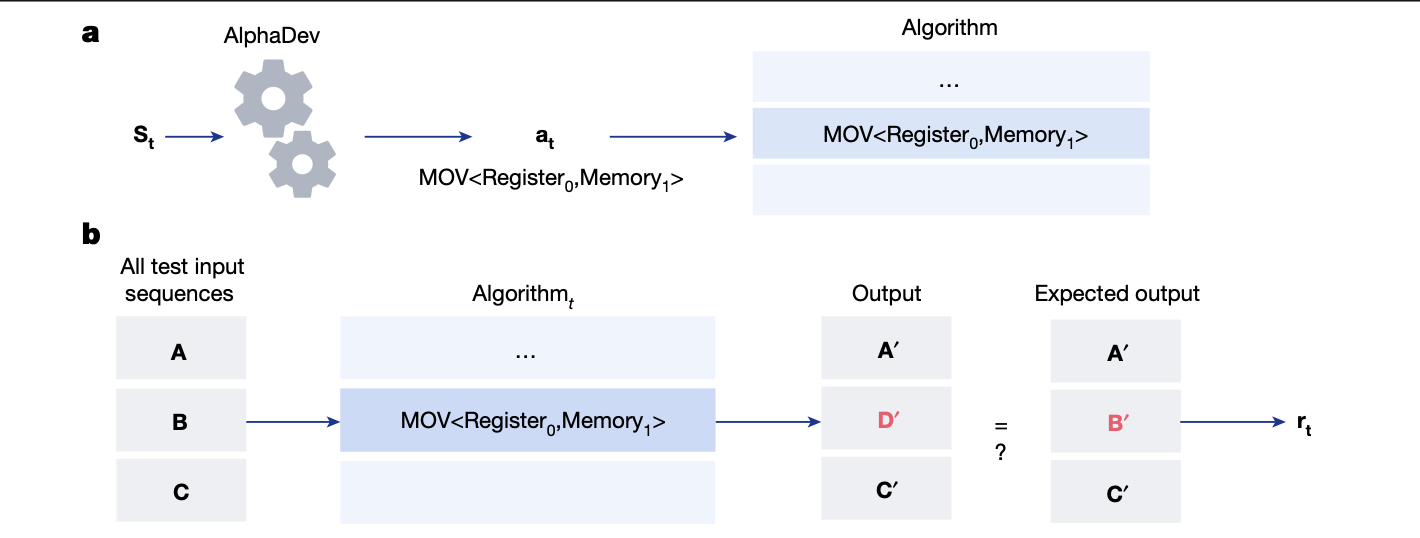
AlphaDev를 통해 살펴볼 수 있는, 머신런닝을 통한 최적화에 최적화 된 케이스는 다음처럼,
1.. 이미 알고리즘과 같은 프로그램을 검증 가능한 Input/Output 테스트 셋을 가지고 있고
2. 해당 테스트 셋으로 검증가능한 범위에서 Algorithm 을 수정하는 것을 학습시키는
경우에 해당할 것이다.
그러나 현실적으로 프로그램들은 그렇지 않다.
결국 AlphaDev에서 보여준 머신런닝 기반의 최적화 방식은 머신런닝을 통해 범용적인 모든 프로그램을 이해하고 스스로 검증 가능한 수준까지 올라와야 열거형 무차별 대입 방식을 대체할 수 있는 방식이 될 것이다.
그렇다면 그런 수준에 이르기까지 학습은 어떻게 시킬 것인가?
광범위한 학습 데이터에 대해 충분히 검증 가능한 Input/Output을 확보한 뒤 학습시키는게 나을까?
아니면, SMT Solver를 연동해 열거형 무차별 대입 방식을 계속 시도시켜서 학습시키는게 나을까?
편향이 있을 수 있지만, 후자 방식에 대한 시도와 결과가 곧 발표되지 않을까 기다려진다.
'Study' 카테고리의 다른 글
| SOUPER 간단 리뷰 (0) | 2024.05.23 |
|---|---|
| superoptimization - 모음 (0) | 2023.07.21 |
| 프로그램 분석 분류 (0) | 2023.05.19 |
| Program Analysis (??) (0) | 2023.05.18 |
| 백업 - Nodejs Uftrace (0) | 2023.03.13 |

